GaoQ's Blog
编程
AI
3D
SEO
关于

坐标系变换

预计阅读时间: 12 分钟

1. 坐标系统

基本概念

实际上，每经过一个矩阵变换，就已经是进入另一个坐标系统了。

1.1 坐标系统类型

1.1.1 物体坐标 (Local Coordinate)

定义
  • 又称局部坐标 (local coordinate or object coordinate)
  • 每个物体建模的时候都有自己的坐标系

1.1.2 世界坐标 (World Coordinate)

定义
  • 3D世界的全局坐标系统
  • 其他的模型都按照这个坐标的位置放置
  • 是经过 model-matrix 转换得到

1.1.3 观察坐标 (View Coordinate)

定义
  • 又称视图坐标、投影坐标、眼坐标 (view coordinate/eye coordinate)
  • 投影就是把坐标转换到相对于观察者的视角下的坐标
  • 以观察者为坐标原点的坐标，经过观察矩阵得到
  • view-matrix 把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标

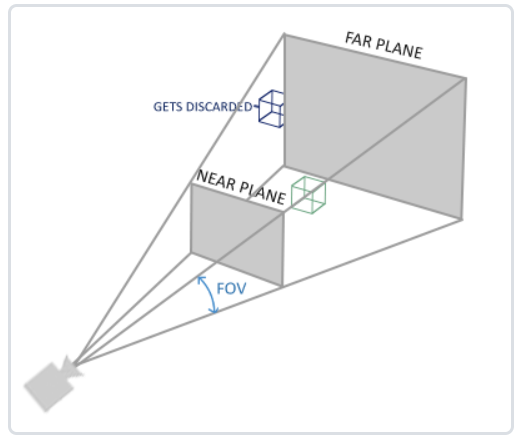
1.1.4 裁剪坐标 (Clip Coordinate)

重要概念
  • 通过 projection-matrix 转换得到
  • 考虑远近平面、FOV以及对z的非线性转换
  • 把特定的坐标转换成标准设备坐标的过程
  • 舍弃标准设备坐标范围外的坐标
  • 投影矩阵与相机的平截头体的参数定义相关
  • 用来计算深度缓冲的变换
深度精度优化
  • 投影矩阵包含了对z值的精度非线性调整
  • 这给了近处的物体很大的深度精度
  • 从观察者视角变换z值的方程嵌入在投影矩阵中
  • 当将顶点坐标从观察空间转到裁剪空间时，这个非线性方程就被应用了
  • 虽然视角上仍然是观察空间的，但是坐标的值已经发生变换，得到的已经是裁剪空间

裁剪坐标示意图

1.1.5 屏幕坐标 (Screen Coordinate)

定义
  • 经过视口变换(viewport transform)得到
  • 最后变换出来的坐标将会送到光栅器
  • 转化为片段，提供给下一阶段使用（片段着色器）
  • 最后得到屏幕像素（和屏幕坐标有区别，屏幕坐标不一定是整数）

1.2 坐标变换流程

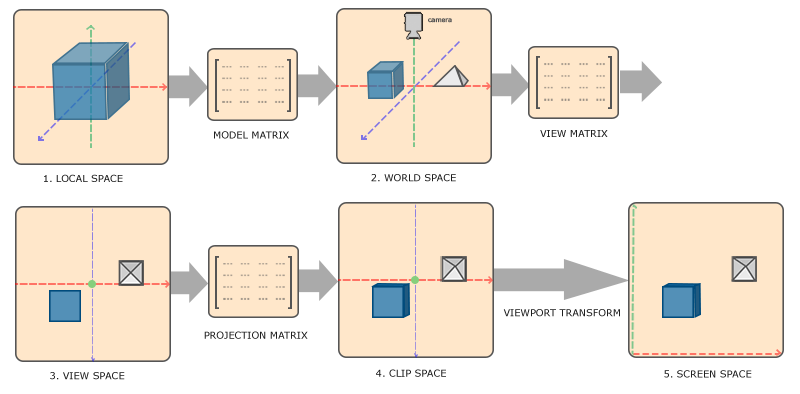
坐标变换流程

渲染管线中的坐标转换

以上1-4步发生在顶点着色器中：

  1. 顶点着色器输出的是经过投影矩阵计算得到的裁剪空间的顶点坐标
  2. 被赋值到顶点着色器中的 gl_Position
  3. 然后进入下一阶段的管线
  4. OpenGL将会自动进行透视除法和裁剪（根据相机定义的远近平面和FOV）
  5. 经过视口变换后，最后才会传递到片元着色器
  6. 片段着色器后才是混合与深度测试（也有提前深度测试，发生在片段着色器之前）

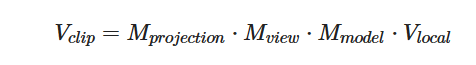
裁剪和NDC坐标

透视除法与裁剪
  • OpenGL对裁剪坐标执行透视除法将它们变换到标准化设备坐标
  • 然后用 glViewPort 内部的参数将标准化设备坐标映射到屏幕坐标
  • 透视除法：顶点着色器之后，OpenGL会自动执行的一步，将xyz向量分别除以齐次向量w
  • 裁剪空间中坐标只是计算了值，并没有进行裁剪
  • 裁剪发生在透视除法之后，超出范围的值会被丢弃
  • 这里具体过程下次复习时，需要结合【十、高级OpenGL】中关于深度的知识

2. 左右手坐标系

Three.js使用右手坐标系

2.1 右手坐标系

  1. 沿着正y轴方向伸出你的右臂，手指着上方
  2. 大拇指指向右方
  3. 食指指向上方
  4. 中指向下弯曲90度

2.2 左手坐标系

  1. 沿着正y轴方向伸出你的左臂，手指着上方
  2. 大拇指指向右方
  3. 食指指向上方
  4. 中指向下弯曲90度
主要区别

左右手坐标系的区别：z轴的方向相反

3. 变换

3.1 向量

定义

向量是有方向有大小的量，具有两个特征：

  • 有大小
  • 有方向
  • 表示的是一个空间的方向

3.2 向量的长度

3.3 向量的运算

3.3.1 向量与标量(常量)运算

基本运算
  • 加减乘除：向量每个分量和标量分别计算，得到新的向量
  • 减和除都只能向量-/标量，标量-/向量没有意义
  • 个人理解的原因：常量是一维的，而向量是多维的，多维可以在每个维度上运算，即多维可以降维，单维无法升维
  • 向量取反：乘-1即可

3.3.2 向量之间的运算

加减法
几何意义
  • 加法：对应的分量加减即可
    • 几何意义：两个向量平移后首尾相连，起点到终点的连线
  • 减法：
    • 几何意义：被减数的向量指向减数向量的连线
向量的乘法
点乘
定义与应用
  • 定义：点乘等于它们的数乘结果（两个向量长度相乘）乘以两个向量之间夹角的余弦值
  • 公式：v⋅k=||v||⋅||k||⋅cosθ
  • 如果两个都是单位向量，则点乘的结果就是两个向量之间夹角的cos值
    • cos0是1，cos90是0，由此可以判断向量是否平行或相交
  • 应用：单位向量的点乘可以用来计算两个向量之间的角度，从而判断垂直
    • 每个分量相乘结果相加，再通过反余弦函数即可求出角度
    • 如果不是单位向量，可以先标准化，再去计算！！

点乘计算

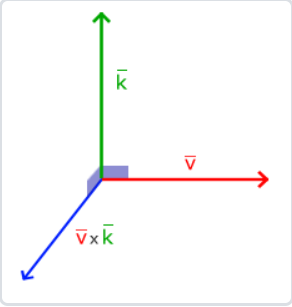
叉乘
特性
  • 需要两个不平行向量作为输入
  • 生成一个正交于两个输入向量的第三个向量
  • 如果输入的两个向量也是正交的，那么叉乘之后将会产生3个互相正交的向量

叉乘示意图

叉乘计算

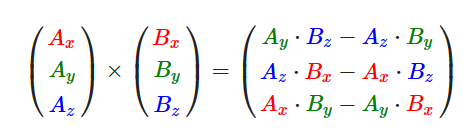
3.4 矩阵

定义

矩阵是一个矩形的数字符号表达式（i行j列），所谓的行列式

3.4.1 矩阵的加减

运算规则

和向量同样的道理，只能矩阵加减标量，或者维度相同的矩阵，才是有意义的

3.4.2 矩阵的数乘

运算规则

每个元素与标量相乘得到新的矩阵，这个标量就相当于一个放大因子

3.4.3 矩阵的乘法

限制条件

两个限制：

  1. 只有当左侧矩阵的列数与右侧矩阵的行数相等，两个矩阵才能相乘

    • 因为乘法的法则是拿左侧矩阵的第n行的每个数分别乘以右侧矩阵的第m列，结果相加，得到坐标为(n,m)的结果
    • 所以：左侧矩阵的每一行的元素个数（列数），需要与右侧矩阵的每一列的元素数量（行数）相等

  2. 矩阵相乘不遵守交换律(Commutative)，也就是不能交换位置

    • 左乘和右乘的结果不同
    • 但是，矩阵遵守乘法结合律，所以可以通过一个矩阵的逆矩阵来求出变换矩阵

矩阵乘法

3.4.4 矩阵与向量相乘

运算规则
  • 向量可以看成N维的矩阵(只有一列) Nx1的矩阵
  • 所以可以和一个MxN的矩阵相乘
  • 单位矩阵: 对角线是1,其他值是0的矩阵

单位矩阵

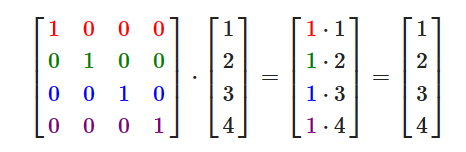
3.4.5 矩阵的作用

Three.js中的实现

three.js中的matrix是一个列秩的数组，索引0，5，10的值是x,y,z的缩放因子

缩放变换
缩放类型
  • 对角线的值就是缩放的分量
  • 均匀缩放：每个缩放的分量相等
  • 不均匀缩放：分量不相等
位移变换
实现方式
  • three.js中的matrix是一个列秩的数组，索引12，13，14的值是x,y,z的位移值
  • 单位矩阵中，使用齐次坐标实现位移
  • 在第4个分量（w）上，书写需要位移的分量，通过矩阵相乘即可
旋转变换
略复杂，使用四元数

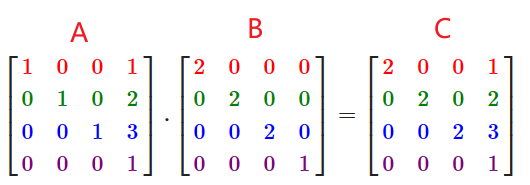
3.4.6 矩阵的组合

强大之处

矩阵变换的力量是可以把多个变换组合到一个矩阵中

矩阵组合示例1

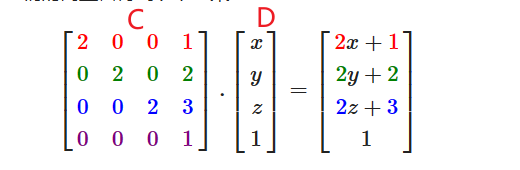
矩阵组合示例2

注意事项

  • 注意1：矩阵的乘法不遵守乘法交换律

    • 所以这里矩阵A * B 得到的结果与向量D相乘，即 A * B * D
    • 由于B离矩阵D最近，所以实际的变换顺序是先应用了矩阵B，然后才是矩阵A
    • 矩阵左乘向量，因为向量总是在最后，所以越在后面的矩阵，越早进行变换

  • 注意2：变换顺序很重要

    • 先缩放再位移和先位移再缩放得到的结果不一样！！
    • 在组合矩阵时，推荐顺序：先进行缩放操作，然后是旋转，最后才是位移
    • 否则它们会（消极地）互相影响。例如，如果你先位移再缩放，位移的向量也会同样被缩放